Angle Between Two Vectors

The angle between two vectors is the angle between their tails. It can be found either by using the dot product (scalar product) or the cross product (vector product). Note that the angle between two vectors always lies between 0° and 180°.

The angle between two vectors is an important concept in mathematics and physics. It helps us understand the relationship between two vectors in terms of their direction and magnitude. Let us learn more about the angle between two vectors both in 2D and 3D along with formula, derivation, and examples.

What is Angle Between Two Vectors?

The angle between two vectors is the angle formed at the intersection of their tails. If the vectors are NOT joined tail-tail then we have to join them from tail to tail by shifting one of the vectors using parallel shifting. The angle can be acute, right, or obtuse, depending on the direction of the vectors. Here are some examples to see how to find the angle between the vectors.

Here, we can see that when the head of a vector is joined to the tail of another vector, the angle formed is NOT the angle between vectors. Instead, one of them should be shifted either in the same direction or parallel to itself such that the tails of vectors are joined with each other in order to measure the angle.

Angle Between Two Vectors Formulas

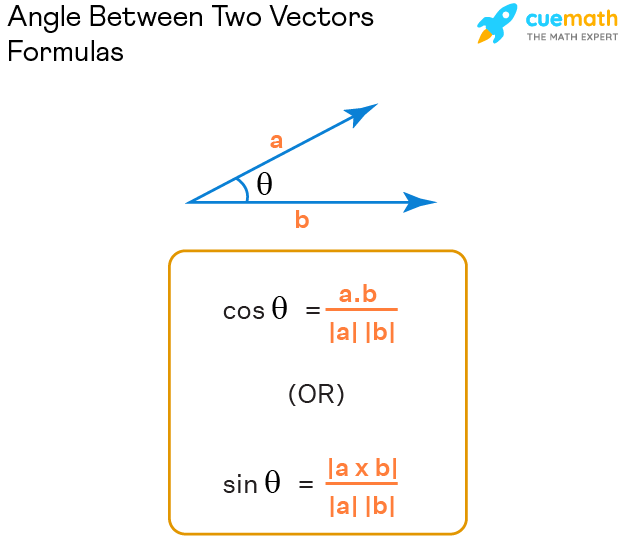
There are two formulas to find the angle between two vectors: one in terms of dot product and the other in terms of the cross product. But the most commonly used formula to find the angle between the vectors involves the dot product (let us see what is the problem with the cross product in the next section). Let a and b be two vectors and θ be the angle between them. Then here are the formulas to find the angle between them using both dot product and cross product:

Angle between two vectors using dot product is, θ = cos^-1 [ (a · b) / (|a| |b|) ]
Angle between two vectors using cross product is, θ = sin^-1 [ |a × b| / (|a| |b|) ]

where a · b is the dot product and a × b is the cross product of a and b. Note that the cross-product formula involves the magnitude in the numerator as well whereas the dot-product formula doesn’t.

Angle Between Two Vectors Using Dot Product

By the definition of dot product, a · b = |a| |b| cos θ. Let us solve this for cos θ. Dividing both sides by |a| |b|.

cos θ = (a · b) / (|a| |b|)

θ = cos^-1 [ (a · b) / (|a| |b|) ]

This is is the formula for the angle between two vectors in terms of the dot product (scalar product). Here, cos^-1 is read as “cos inverse” and it is called “inverse cosine function“.

Angle Between Two Vectors Using Cross Product

By the definition of cross product, a × b = |a| |b| sin θ n^. To solve this for θ, let us take magnitude on both sides. Then we get

|a × b| = |a| |b| sin θ |n^|.

We know n^ is a unit vector and hence its magnitude is 1. So

|a × b| = |a| |b| sin θ

Dividing both sides by |a| |b|.

sin θ = |a × b| / (|a| |b|)

θ = sin^-1 [ |a × b| / (|a| |b|) ]

This is is the formula for the vector angle in terms of the cross product (vector product). This formula causes some ambiguity (which we discuss in the next section) and is not a popular formula to use to find angle between vectors. Here, sin^-1 is read as “sin inverse” and it is called “inverse sine function“.

Finding Angle Between Two Vectors

Let us see some examples of finding the angle between two vectors using dot product in both 2D and 3D. Let us also see the ambiguity caused by the cross-product formula to find the angle between two vectors.

Angle Between Two Vectors in 2D

Let us consider two vectors in 2D say a = <1, -2> and b = <-2, 1>. Let θ be the angle between them. Let us find the angle between vectors using both dot product and cross product and let us see what is the ambiguity that a cross product can cause.

Angle Between Vectors in 2D Using Dot Product

Let us compute the dot product and magnitudes of both vectors.

a · b = <1, -2> ·<-2, 1> = 1(-2) + (-2)(1) = -2 – 2 = -4.
|a| = √(1)² + (-2)² = √1 + 4 = √5
|b| = √(-2)² + (1)² = √4 + 1 = √5

By using the angle between two vectors formula using dot product, θ = cos^-1 [ (a · b) / (|a| |b|) ].

Then θ = cos^-1 (-4 / √5 · √5) = cos^-1 (-4/5)

We can either use a calculator to evaluate this directly or we can use the formula cos^-1(-x) = 180° – cos^-1x and then use the calculator (whenever the dot product is negative using the formula cos^-1(-x) = 180° – cos^-1x is very helpful as we know that the angle between two vectors always lies between 0° and 180°). Then we get:

cos^-1 (-4/5) ≈ 143.13°

Angle Between Vectors in 2D Using Cross Product

Let us compute the cross product of a and b.

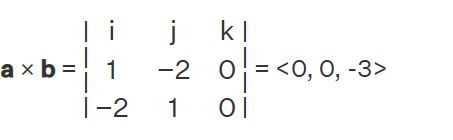Now we find its magnitude.

|a × b| = √(0)² + (0)² + (-3)² = 3

By using the angle between two vectors formula using cross product, θ = sin^-1 [ |a × b| / (|a| |b|) ].

Then θ = sin^-1 (3 / √5 · √5) = sin^-1 (3/5)

If we use the calculator to calculate this, θ ≈ 36.87 (or) 180 – 36.87 (as sine is positive in the second quadrant as well). So

θ ≈ 36.87 (or) 143.13°.

Thus, we got two angles and there is no evidence to choose one of them to be the angle between vectors a and b. Thus, the cross-product formula may not be helpful all the time to find the angle between two vectors.

Angle Between Two Vectors in 3D

Let us consider an example to find the angle between two vectors in 3D. Let a = i + 2j + 3k and b = 3i – 2j + k. We will compute the dot product and the magnitudes first:

a · b = <1, 2, 3> ·<3, -2, 1> = 1(3) + (-2)(-2) + 3(1) = 3 – 4 + 3 = 2.
|a| = √(1)² + (2)² + 3² = √1 + 4 +9 = √14
|b| = √(3)² + (-2)² + 1² = √9 + 4 + 1 = √14

We have θ = cos^-1 [ (a · b) / (|a| |b|) ].

Then θ = cos^-1 (2 / √14 · √14) = cos^-1 (2 / 14) = cos^-1 (1/7) ≈ 81.79°.

Important Points on Angle Between Two Vectors:

The angle (θ) between two vectors a and b is found with the formula θ = cos^-1 [ (a · b) / (|a| |b|) ].
The angle between two equal vectors is 0 degrees as θ = cos^-1 [ (a · a) / (|a| |a|) ] = cos^-1 (|a|²/|a|²) = cos^-11 = 0°.
The angle between two parallel vectors is 0 degrees as θ = cos^-1 [ (a · ka) / (|a| |ka|) ] = cos^-1 (k|a|²/k|a|²) =cos^-1 1 = 0°.
The angle(θ) between two vectors a and b using the cross product is θ = sin^-1 [ |a × b| / (|a| |b|) ].
For any two vectors a and b, if a · b is positive, then the angle lies between 0° and 90°;
if a · b is negative, then the angle lies between 90° and 180°.
The angle between each of the two vectors among the unit vectors i, j, and k is 90°.